Перейти к:
Исследование колебаний композитного магнитоэлектроупругого биморфа в зависимости от объемных долей его компонентов на основе прикладной теории
https://doi.org/10.23947/2687-1653-2022-22-1-4-13
Аннотация
Введение. Исследованы поперечные колебания биморфа, состоящего из двух пьезомагнитоэлектрических слоев и находящегося в переменном магнитном поле. Пьезомагнитоэлектрические слои представляют собой многослойный композит с чередующимися пьезоэлектрическими и пьезомагнитными слоями. Механические и физические свойства такого композита задаются известными эффективными константами.
Материалы и методы. Прикладная теория колебаний многослойной пластины учитывает нелинейное распределение электрического и магнитного потенциала в пьезоактивных слоях в продольном и поперечном направлениях. На основе указанной теории исследованы напряженно-деформированное состояние, зависимости прогиба, электрического и магнитного потенциалов от объемного соотношения состава шарнирно опертого биморфа. Электрический потенциал принят равным нулю на всех электродах, магнитный равен нулю на внутренней границе и неизвестен на внешних. Поэтому распределение электрического и магнитного потенциалов в середине слоя — неизвестные функции. В случае магнитного потенциала распределение на внешней границе также неизвестно. В задаче были приняты гипотезы Кирхгофа для механических характеристик. Использование вариационного принципа и квадратичной зависимости электрического и магнитного потенциалов по толщине пьезоактивных слоев позволило получить систему дифференциальных уравнений и граничных условий.
Результаты исследования. При изменении объемного соотношения состава пьезоактивных материалов биморфа электрический потенциал в середине слоя нелинейно изменяется. Магнитный потенциал в середине слоя и на внешней границе практически линейно увеличивается с увеличением объемного процента BaTiO3. Определена зависимость прогиба в середине слоя.
Обсуждение и заключения. Построена прикладная теория расчета поперечных колебаний биморфа с двумя пьезомагнитоэлектрическими слоями. Исследована зависимость характеристик напряженно-деформированного состояния, электрического и магнитного полей от объемных долей пьезомагнитного и пьезоэлектрического материалов.
Ключевые слова
Для цитирования:
Соловьев А.Н., До Т., Чебаненко В.А., Лесняк О.Н., Кириллова Е.В. Исследование колебаний композитного магнитоэлектроупругого биморфа в зависимости от объемных долей его компонентов на основе прикладной теории. Advanced Engineering Research (Rostov-on-Don). 2022;22(1):4-13. https://doi.org/10.23947/2687-1653-2022-22-1-4-13
For citation:
Soloviev A.N., Do T., Chebanenko V.A., Lesnyak O.N., Kirillova E.V. Vibration analysis of a composite magnetoelectroelastic bimorph depending on the volume fractions of its components based on applied theory. Advanced Engineering Research (Rostov-on-Don). 2022;22(1):4-13. https://doi.org/10.23947/2687-1653-2022-22-1-4-13
Введение. При производстве сенсорных и измерительных систем, малогабаритных бытовых приборов, сотовых телефонов и беспроводных сенсорных систем для мониторинга и диагностики технического состояния объектов не нужны мощные источники энергии. При этом обязательными условиями являются мобильность и энергонезависимость вышеперечисленных устройств.
Пьезоэлектрические материалы напрямую преобразуют электрическую энергию в механическую и обратно. Это свойство позволяет широко использовать их в науке и технике. Данные материалы задействуют в ультразвуковых излучателях упругих и акустических волн, приемниках таких волн, устройствах подавления колебаний элементов машин и конструкций и т. п. В последнее время бурно развивается еще одна область применения пьезоэлектриков — устройства сбора и накопления энергии. В этом случае пьезоэлектрические материалы входят в состав пьезоэлектрических генераторов энергии (ПЭГ). ПЭГ помещаются на элементах машин или конструкций, которые интенсивно колеблются, находятся в зоне прохождения упругих волн или подвержены действию переменного давления. Основные типы этих устройств имеют биморфную или стековую многослойную структуру и испытывают изгибные или продольные деформации соответственно. На основе ПЭГ создаются маломощные источники электрического тока. В их числе — автономные источники питания (например, для устройств мониторинга повреждений в труднодоступных местах сооружений трубопроводов и т. п.). Обзор таких устройств есть в [1–2]. Один из способов конструировать эффективные ПЭГ — использование пьезоактивных композитов различного типа связности и неоднородных материалов на основе пьезокерамики, в том числе пористой.
Фиксировать или задействовать энергию переменного магнитного поля могут ПЭГ, в конструкции которых есть дополнительные электромагнитные элементы или постоянные магниты. Один из путей решения данной задачи — использование пьезомагнитных материалов в сочетании с пьезоэлектрическими. В этом случае переменное магнитное поле приводит к деформации пьезомагнетика и связанного пьезоэлектрика, в результате последний генерирует электрическую энергию. Существует класс материалов, обладающих пьезомагнитными свойствами. Пьезомагнетизм — это явление, наблюдаемое в некоторых антиферромагнитных и ферромагнитных кристаллах. Он характеризуется линейной связью между магнитной поляризацией системы и механической деформацией. В пьезомагнитном материале можно вызвать спонтанный магнитный момент, приложив механическое напряжение, или деформацию, приложив магнитное поле. В исследованиях пьезомагнитных материалов очень часто рассматривается CoFe2O4 [3–5]. В [6–8] исследуется композит на основе CoFe2O4 и BaTiO3, обладающий пьезоэлектрическими и пьезомагнитными свойствами одновременно. Решения задач электроупругости и магнитоупругости приведены в [9–11]. В [12] развиты прикладные теории колебаний многослойных пьезоэлектрических пластин с учетом специфики распределения электрического потенциала по толщине конструкции.
Задачи об установившихся колебаниях электромагнитоупругого слоя и полупространства под действием гармонических нагрузок представлены в [13][14]. Учтены предварительные напряжения, а также различные электрические и магнитные условия на границах. Исследовано влияние указанных факторов на дисперсионные свойства.
Ранее [15][16] была разработана прикладная теория, которая учитывает неоднородное распределение электрического потенциала в продольном направлении и квадратичную зависимость по толщине. В этих же работах исследовано напряженно-деформированное и электрическое состояние шарнирно опертого и консольно закрепленного биморфа. В обоих случаях прикладная теория показала хорошую сходимость с результатами конечноэлементного моделирования. Авторы также получили прикладную теорию колебаний биморфа [17], состоящего из электроупругого и магнитоупругого слоя. Этот подход хорошо согласуется с результатами конечноэлементного анализа.
В данной работе рассматриваются колебания устройства в рамках плоской деформации. На основе вариационного принципа построена прикладная теория изгибных колебаний двухслойного пьезомагнитоэлектрического биморфа. Для установившихся колебаний получены граничные условия и система дифференциальных уравнений для четырех неизвестных функций (прогиб, электрический потенциал в середине слоя, магнитный потенциал в середине слоя и на внешней границе), зависящих от длины биморфа.
Исследовано влияние разных процентных объемных соотношений состава биморфа на прогиб, электрический и магнитный потенциалы в определенных положениях. Результаты исследования позволяют выбрать состав композиционного пьезомагнитоэлектрического материала для достижения наиболее эффективной работы устройства.
Материалы и методы. Рассматривается пластина, состоящая из двух одинаковых пьезомагнитоэлектрических слоев. Она совершает установившиеся поперечные колебания в рамках плоской деформации. Каждый слой представляет собой композит 2–2 связности, состоящий из чередующихся пьезоэлектрических и пьезомагнитных слоев (рис. 1).

Рис. 1. Структура композита 2–2
В [8] найдены эффективные свойства такого композита. Большие поверхности слоев электродированы, а сами слои поляризованы по толщине. Биморф шарнирно закреплен по краям, все поверхности свободны от механических напряжений. На верхнюю и нижнюю границы пластины воздействует магнитный поток B0, в то время как на границе между слоями магнитный потенциал считается равным нулю. Электрический потенциал равен нулю на всех электродах. Боковые поверхности считаются изолированными от магнитных и электрических полей.
Уравнения для описания колебаний композита с эффективными свойствами, связностью механических, электрических и магнитных полей, имеют вид [18]:
 (1)
(1)
Здесь σ и ε — тензоры механических напряжений и деформации, D и E — векторы электрической индукции и напряженности электрического поля, B и H — векторы магнитной индукции и напряженности магнитного поля, ρ — плотность материала, c — тензор упругих модулей, e — тензор пьезоэлектрических модулей, h — тензор пьезомагнитных модулей, κ — тензор диэлектрических проницаемостей, α — тензор магнитоэлектрических модулей, μ — тензор магнитных проницаемостей, f — вектор плотности массовых сил, σΩ — объемная плотность электрических зарядов, u — вектор перемещений, φ и ξ — электрический и магнитный потенциалы.
Граничные условия определяются для механического, электрического и магнитного поля соответственно.
Для первого случая отметим отсутствие механических напряжений на границе биморфа:

Биморф шарнирно закреплен на концах (рис. 2):

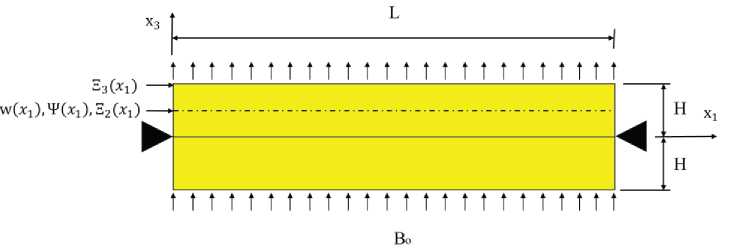
Рис. 2. Геометрия и граничные условия биморфа с композитными пьезомагнитоэлектрическими слоями
Далее сформулируем электрические граничные условия. Электрический потенциал на внутреннем и на внешнем электроде соответственно:

Укажем магнитные граничные условия. Магнитный потенциал на внутренней границе:
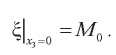
Магнитный поток B0 воздействует на верхнюю и нижнюю границы пластины:
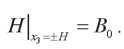
Воспользуемся вариационным уравнением для установившихся колебаний [10]. Оно обобщает принцип Гамильтона в теории электроупругости с учетом магнитных составляющих. Для случая плоской деформации при отсутствии поверхностных нагрузок и при наличии магнитного потока:
 (2)
(2)
Для построения прикладной теории колебаний примем гипотезы Кирхгофа. В соответствии с ними распределение перемещений по толщине имеет вид:
 (3)
(3)
В частности, для механического поля принята гипотеза единой нормали. Далее рассматривается задача, в которой значение электрического потенциала на электродах может быть равно нулю, поэтому его распределение не описывается линейной функцией. С учетом возможной неоднородности по длине элемента, связанной с влиянием граничных условий на концах биморфа, его распределение по толщине принимается квадратичным:
 (4)
(4)
Здесь  . Функции V0, V1 и V2 отвечают за значение электрического потенциала на внутреннем электроде, в середине слоя и на внешнем электроде соответственно. Чтобы удовлетворить условиям задачи, примем эти функции в следующем виде (см. рис. 2):
. Функции V0, V1 и V2 отвечают за значение электрического потенциала на внутреннем электроде, в середине слоя и на внешнем электроде соответственно. Чтобы удовлетворить условиям задачи, примем эти функции в следующем виде (см. рис. 2):
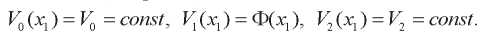
Здесь функция Ф(x1) является неизвестной.
Представим квадратичное распределение магнитного потенциала по толщине каждого слоя. Распределение по длине неоднородно, на внутренней границе слоев его значение принимается равным нулю:
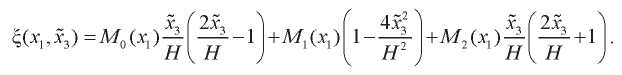 (5)
(5)
Здесь  . Функции M0, M1 и M2 отвечают за значение магнитного потенциала на внутренней границе, в середине слоя и на внешней границе соответственно и принимаются в следующем виде (рис. 2):
. Функции M0, M1 и M2 отвечают за значение магнитного потенциала на внутренней границе, в середине слоя и на внешней границе соответственно и принимаются в следующем виде (рис. 2):
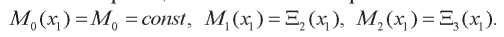
Здесь функции 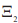 (x1) и
(x1) и  (x1) являются неизвестными.
(x1) являются неизвестными.
Соотношения (3)–(5) подставим в уравнение (2) и проинтегрируем его по толщине биморфа, а затем приравняем к нулю коэффициенты при независимых вариациях δw, δФ, 2 δ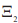 и 3 δ
и 3 δ . Тем самым мы получаем систему из четырех дифференциальных уравнений (6) от четырех неизвестных функций, зависящих от x1 (далее опустим нижний индекс), и пять граничных условий (7).
. Тем самым мы получаем систему из четырех дифференциальных уравнений (6) от четырех неизвестных функций, зависящих от x1 (далее опустим нижний индекс), и пять граничных условий (7).


Результаты исследования. Сопоставлены результаты расчета биморфа по предложенной теории с конечноэлементным расчетом в низкочастотной области для соотношения объемных долей пьезоэлектрического и пьезомагнитного компонентов 80 % BaTiO3 и 20 % CoFe2O4. Сравнение показало, что погрешность в нахождении характеристик механического и магнитного полей менее 1 %. При определении электрического поля в средней части пластины разница составила порядка 5 %. Описывая ситуацию в окрестности точек опоры, следует отметить, что размер окрестности по продольной координате приблизительно равен толщине биморфа. Здесь при определении электрического поля зафиксирована разница 20 %.
Первым шагом исследования колебания двухслойного пьезомагнитоэлектрического биморфа при изменении объемного соотношения BaTiO3 и CoFe2O4 в составе композита является определение его эффективных свойств. В таблицах 1 и 2 представлены эти свойства, найденные по результатам работы [8].
Таблица 1
Материальные константы (упругие модули, диэлектрические и магнитные проницаемости) для различной объемной доли BaTiO3
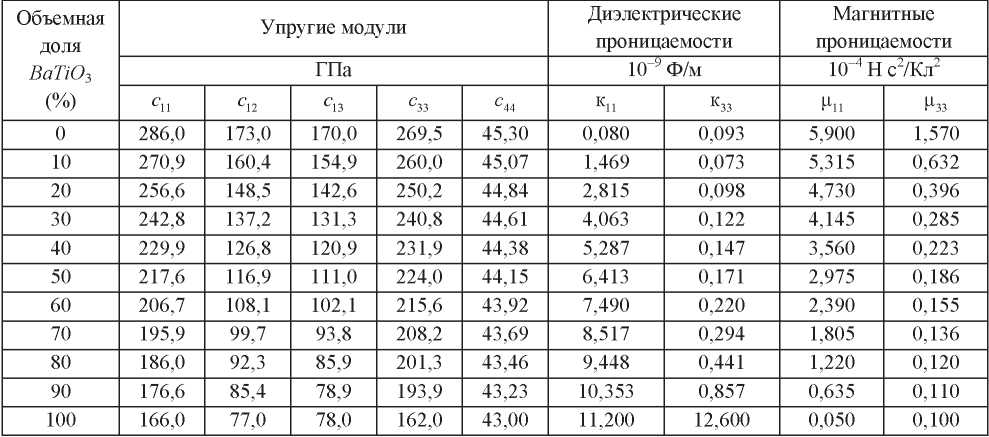
Таблица 2
Материальные константы (пьезоэлектрические, пьезомагнитные и магнитоэлектрические модули) для различной объемной доли BaTiO3
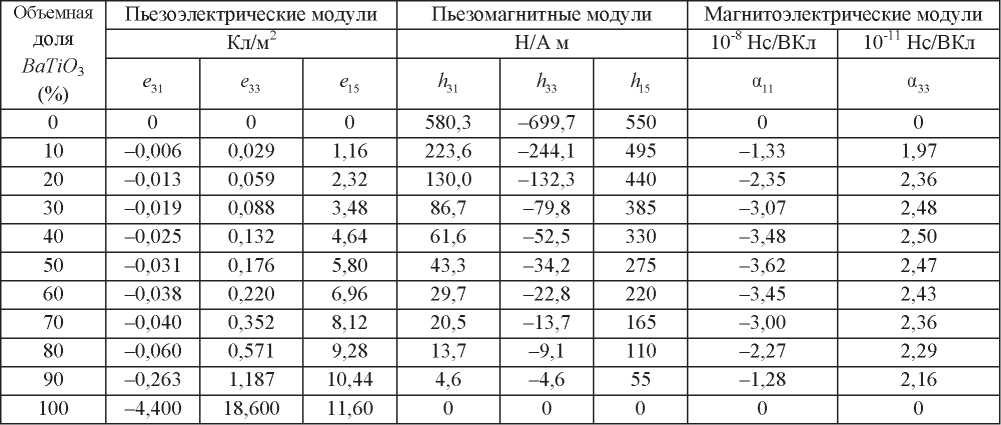
Колебания биморфа возбуждались магнитным потоком, приложенным к верхней и нижней граням (рис. 2), который изменялся по гармоническому закону с амплитудой B0=5*10-5 Вб и частотой 10 кГц.
На рис. 3 представлен прогиб в середине слоя в зависимости от объемной доли BaTiO3. Из графика видно, что прогиб в положении, имеющем координаты 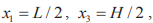 , равен нулю, если биморф состоит только из пьезоэлектрика BaTiO3. Прогиб биморфа достигает наибольшего значения, если в его составе только пьезомагнетик CoFe2O4. Прогиб практически линейно зависит от объемного соотношения составляющих пьезоактивных материалов.
, равен нулю, если биморф состоит только из пьезоэлектрика BaTiO3. Прогиб биморфа достигает наибольшего значения, если в его составе только пьезомагнетик CoFe2O4. Прогиб практически линейно зависит от объемного соотношения составляющих пьезоактивных материалов.

Рис. 3. Прогиб w(x1) в середине слоя для различной объемной доли BaTiO3
На основе данных рис. 4 можно сделать заключение, что электрический потенциал в середине слоя нелинейно изменяется при изменении объемного соотношения состава пьезоактивных материалов биморфа. Если биморф состоит только из BaTiO3 либо CoFe2O4, то электрический потенциал в точке (L / 2, Н / 2) равен нулю и достигает наибольшего значения при 35 % BaTiO3 в составе биморфа.
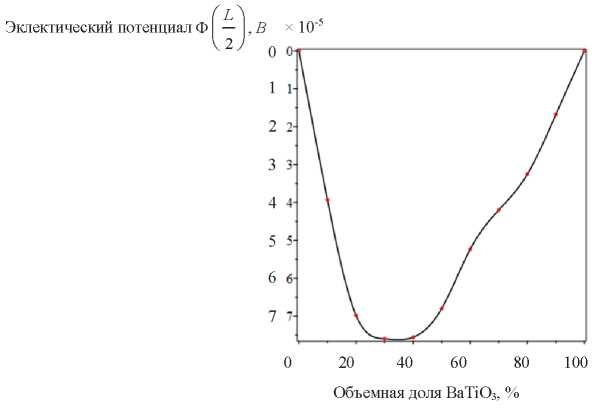
Рис. 4. Электрический потенциал 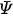 (x1) для различной объемной доли BaTiO3
(x1) для различной объемной доли BaTiO3
Анализ рис. 5 и 6 позволяет сделать заключение, что магнитный потенциал в середине слоя 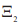 (L / 2) и на внешней границе
(L / 2) и на внешней границе 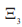 (L / 2) практически линейно увеличивается с ростом объема BaTiO3 в составе биморфа.
(L / 2) практически линейно увеличивается с ростом объема BaTiO3 в составе биморфа.
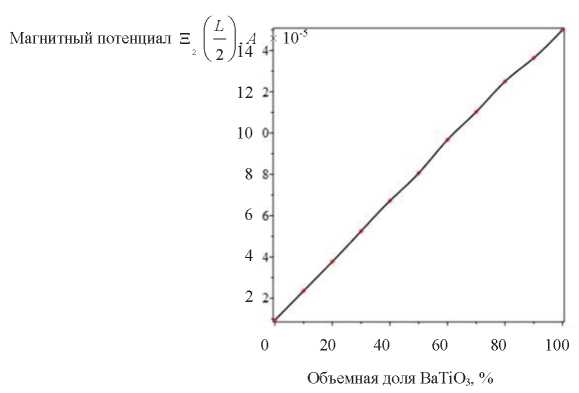
Рис. 5. Магнитный потенциал 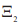 (L / 2) для различной объемной доли BaTiO3
(L / 2) для различной объемной доли BaTiO3
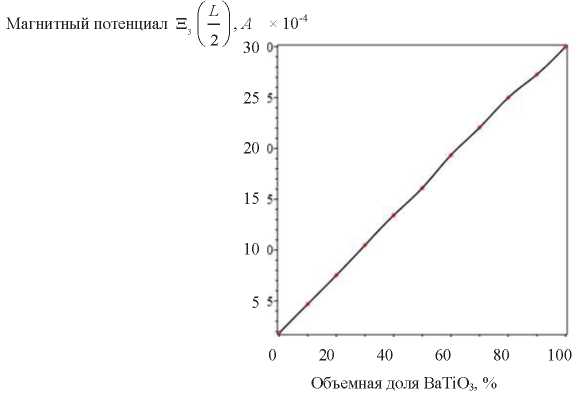
Рис. 6. Магнитный потенциал 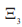 (L / 2) для различной объемной доли BaTiO3
(L / 2) для различной объемной доли BaTiO3
Обсуждение и заключения. Предложена прикладная теория для расчета поперечных колебаний биморфа из двух слоев композита на основе CoFe2O4 и BaTiO3, обладающего одновременно пьезоэлектрическими и пьезомагнитными свойствами, в переменном магнитном поле. Такая конструкция может служить моделью пьезоэлектрического генератора устройства сбора и накопления энергии при действии внешнего магнитного поля. В низкочастотной области (ниже собственной частоты первой изгибной моды) проведены расчеты напряженно-деформированного состояния биморфа, распределения электрического и магнитного полей. Исследована зависимость прогиба, электрического и магнитного потенциалов от объемного соотношения состава биморфа. В дальнейшей работе предполагается определить выходной потенциал и мощность электрического тока, возбуждаемого переменным магнитным полем. Целью этих изысканий будет сбор электрической энергии.
Список литературы
1. Gaudenzi, P. Smart structures: physical behavior, mathematical modeling and applications / Paolo Gaudenzi. — New York : John Wiley & Sons, 2009. — 194 p. https://doi.org/10.1002/9780470682401
2. A review of smart materials: Researches and applications / I. N. Qader, M. Kok, F. Dagdelen, Y. Aydogdu // El-Cezeri Journal of Science and Engineering. — 2019. — Vol. 6. — P. 755–788. https://doi.org/10.31202/ecjse.562177
3. Crafting the multiferroic BiFeO3 -CoFe2O4 nanocomposite for next-generation devices: A review / T. Amrillah, A. Hermawan, C. P. Wulandari [et al.] // Materials and Manufacturing Processes. — 2021. — Vol. 36. — P. 1579–1596. https://doi.org/10.1080/10426914.2021.1945096
4. Tunable maximum energy product in CoFe2O4 nanopowder for permanent magnet application / B. Abraime, A. Mahmoud, F. Boschini [et al.] // Journal of Magnetism and Magnetic Materials. — 2018. — Vol. 467. — P. 129–134. https://doi.org/10.1016/j.jmmm.2018.07.063
5. Size effect on the magnetic properties of CoFe2O4 nanoparticles: a Monte Carlo study / R. Lamouri, O. Mounkachi, E. Salmani [et al.] // Ceramics International. — 2020. — Vol. 46. — P. 8092–8096. https://doi.org/10.1016/j.ceramint.2019.12.035
6. Kim, J.-Y. Micromechanical analysis of effective properties of magneto-electro-thermo-elastic multilayer composites / Jin-Yeon Kim // International Journal of Engineering Science. — 2011. — Vol. 49. — P. 1001–1018. https://doi.org/10.1016/j.ijengsci.2011.05.012
7. Siva, K. V. Improved room temperature magnetoelectric response in CoFe2O4-BaTiO3 core shell and bipolar magnetostrictive properties in CoFe2O4 / K. V. Siva, P. Kaviraj, A. Arockiarajan // Materials Letters. — 2020. Vol. 268. — Art. 127623. https://doi.org/10.1016/j.matlet.2020.127623
8. Challagulla, K. S. Micromechanical analysis of magneto-electro-thermo-elastic composite materials with applications to multilayered structures / K. S. Challagulla, A. V. Georgiades // International Journal of Engineering Science. — 2011. — Vol. 49. — P. 85–104. https://doi.org/10.1016/j.ijengsci.2010.06.025
9. Новацкий, В. Электромагнитные эффекты в твердых телах / В. Новацкий, В. А. Шачнев. — Москва : Мир, 1986. — 160 с.
10. Партон, В. З. Электромагнитоупругость пьезоэлектрических и электропроводных тел / В. З. Партон, Б. А. Кудрявцев // Москва : Наука, 1988. — 472 с.
11. Багдасaрян, Г. Е. Электромагнитоупругие волны / Г. Е. Багдасaрян, З. Н. Даноян. — Ереван : Изд-во Ереванского государственного университета, 2006. — 492 с.
12. Vatul'yan, A. O. Flexural vibrations of a piezoelectric bimorph with a cut internal electrode / A. O. Vatul'yan, A. A. Rynkova // Journal of Applied Mechanics and Technical Physics. — 2001. — Vol. 42. — P. 164–168. https://doi.org/10.1023/A:1018837401827
13. Levi, M. O. Some features of the dynamics of electro-magneto-elastic half-space with initial deformations / M. O. Levi, V. V. Kalinchuk // In: Proc. 2017 Dynamics of Systems, Mechanisms and Machines (Dynamics), IEEE. 2017. — P. 262–266. https://ieeexplore.ieee.org/document/8239478
14. Влияние граничных условий на динамику электромагнитоупругой полуограниченной среды / М. О. Леви, И. Е. Анджикович, Е. И. Ворович, И. Б. Михайлова // Вестник Южного научного центра РАН. 2012. — T. 8, № 4. — C. 14–19.
15. Applied theory of bending vibrations of a piezoelectric bimorph with a quadratic electric potential distribution / A. N. Soloviev, V. A. Chebanenko, I. A. Parinov, P. A. Oganesyan // Materials Physics and Mechanics. 2019. — Vol. 42. — P. 65–73. https://doi.org/10.18720/MPM.4212019_7
16. Исследование колебаний биморфной пластины с учетом нелинейности электрического потенциала / А. Н. Соловьев, В. А. Чебаненко, И. А. Паринов, П. А. Оганесян // Наука Юга России. — 2019. — Т. 15, № 3. С. 3–11. https://doi.org/10.7868/S25000640190301
17. Applied theory of bending vibration of the piezoelectric and piezomagnetic bimorph / Do Thanh Binh, V. A. Chebanenko, Le Van Duong [et al.] // Journal of Advanced Dielectrics. — 2020. — Vol. 10. — Art. 2050007. https://doi.org/10.1142/S2010135X20500071
18. Finite element approach for composite magneto-piezoelectric materials modeling in ACELAN-COMPOS package / N. V. Kurbatova, D. K. Nadolin, A. V. Nasedkin [et al.] // In book: Analysis and Modelling of Advanced Structures and Smart Systems. — 2018. — Vol. 81. — P. 69–88. https://doi.org/10.1007/978-981-10-6895-9_5
Об авторах
А. Н. СоловьевРоссия
Соловьев Аркадий Николаевич, заведующий кафедрой «Теоретическая и прикладная механика», доктор физико-математических наук, профессор
344003, г. Ростов-на-Дону, пл. Гагарина, 1
Тхань Бинь До
Россия
аспирант кафедры «Теоретическая и прикладная механика»
344003, г. Ростов-на-Дону, пл. Гагарина, 1
В. А. Чебаненко
Россия
Чебаненко Валерий Александрович, старший научный сотрудник, кандидат физико-математических наук, старший научный сотрудник
344010, г. Ростов-на-Дону, ул. Чехова, 41
О. Н. Лесняк
Россия
Лесняк Ольга Николаевна, доцент кафедры «Теоретическая и прикладная механика», кандидат технических наук, доцент
344003, г. Ростов-на-Дону, пл. Гагарина, 1
Е. В. Кириллова
Германия
Кириллова Евгения Вадимовна, кандидат физико-математических наук, профессор
65197, г. Висбаден, Курт-Шумахер-Кинг, 18
Рецензия
Для цитирования:
Соловьев А.Н., До Т., Чебаненко В.А., Лесняк О.Н., Кириллова Е.В. Исследование колебаний композитного магнитоэлектроупругого биморфа в зависимости от объемных долей его компонентов на основе прикладной теории. Advanced Engineering Research (Rostov-on-Don). 2022;22(1):4-13. https://doi.org/10.23947/2687-1653-2022-22-1-4-13
For citation:
Soloviev A.N., Do T., Chebanenko V.A., Lesnyak O.N., Kirillova E.V. Vibration analysis of a composite magnetoelectroelastic bimorph depending on the volume fractions of its components based on applied theory. Advanced Engineering Research (Rostov-on-Don). 2022;22(1):4-13. https://doi.org/10.23947/2687-1653-2022-22-1-4-13




































