Scroll to:
Vibration analysis of a composite magnetoelectroelastic bimorph depending on the volume fractions of its components based on applied theory
https://doi.org/10.23947/2687-1653-2022-22-1-4-13
Abstract
Introduction. Transverse vibrations of a bimorph consisting of two piezomagnetoelectric layers and located in the alternating magnetic field are investigated. Piezomagnetoelectric layers are multilayer composites with alternating piezoelectric and piezomagnetic layers. The mechanical and physical properties of such a composite are given by known effective constants.
Materials and Methods. The applied theory of multilayer plate vibrations takes into account the nonlinear distribution of electric and magnetic potential in piezoactive layers in the longitudinal and transverse directions. On the basis of this theory, the stress-strain state, the dependences of deflection, electric and magnetic potentials on the volume ratio of the composition of the hinged bimorph, are investigated. The electric potential is assumed to be zero at all electrodes, while the magnetic potential is zero at the inner boundary and unknown at the outer boundaries. Therefore, the distribution of electric and magnetic potentials in the middle of the layer are unknown functions. In the case of the magnetic potential, the distribution at the outer boundary is also unknown. In the problem, the Kirchhoff hypotheses for mechanical characteristics were accepted. The use of the variational principle and the quadratic dependence of the electric and magnetic potentials on the thickness of piezoactive layers made it possible to obtain a system of differential equations and boundary conditions.
Results. When the volume ratio of the composition of piezoactive bimorph materials changes, the electric potential in the middle of the layer changes nonlinearly. The magnetic potential in the middle of the layer and at the outer boundary increases almost linearly with an increase in the volume percentage of BaTiO3. The dependence of the deflection in the middle of the layer is determined.
Discussion and Conclusions. An applied theory for calculating transverse vibrations of a bimorph with two piezomagnetoelectric layers is constructed. The dependence of the characteristics of the stress-strain state, electric and magnetic fields on the volume fractions of piezomagnetic and piezoelectric materials, is investigated.
Keywords
For citations:
Soloviev A.N., Do T., Chebanenko V.A., Lesnyak O.N., Kirillova E.V. Vibration analysis of a composite magnetoelectroelastic bimorph depending on the volume fractions of its components based on applied theory. Advanced Engineering Research (Rostov-on-Don). 2022;22(1):4-13. https://doi.org/10.23947/2687-1653-2022-22-1-4-13
Introduction. In the production of sensor and measuring systems, small household appliances, cell phones, and wireless sensor systems, powerful energy sources are not needed to monitor and diagnose the technical condition of objects. In this case, the prerequisites are the mobility and volatility of the above devices.
Piezoelectric materials directly convert electrical energy into mechanical energy and vice versa. This property allows them to be widely used in science and technology. These materials are used in ultrasonic emitters of elastic and acoustic waves, receivers of such waves, devices for suppressing vibrations of machine elements and structures, etc. Recently, another field of application of piezoelectrics has been rapidly developing — energy collection and storage devices. In this case, piezoelectric materials are part of piezoelectric energy generators (PEG). PEG are placed on elements of machines or structures that vibrate intensively, which are in the zone of elastic wave propagation or are exposed to variable pressure. The main types of these devices have a bimorph or stack multilayer structure and experience bending or longitudinal deformations, respectively. Low-power sources of electric current are created on the basis of PEG. They include autonomous power sources (e.g., for damage monitoring devices in hard-to-reach places of pipeline structures, etc.). An overview of such devices is available in [1–2]. One of the ways to design effective PEG is the use of piezoactive composites of various types of connectivity and heterogeneous materials based on piezoceramics, including porous one.
PEG, in whose design there are additional electromagnetic elements or permanent magnets, can fix or use the energy of an alternating magnetic field. One of the ways to solve this problem is the use of piezomagnetic materials in combination with piezoelectric ones. In this case, the alternating magnetic field causes the deformation of the piezomagnetic and the coupled piezoelectric, as a result, the latter generates electrical energy. There is a class of materials with ferromagnetic properties. Piezomagnetism is a phenomenon observed in some antiferromagnetic and ferromagnetic crystals. It is characterized by a linear relationship between the magnetic polarization of the system and mechanical deformation. In a piezomagnetic material, a spontaneous magnetic moment can be induced through applying mechanical stress, or deformation by applying a magnetic field. In studies of piezomagnetic materials [3–5], CoFe2O4 is very often considered. In [6–8], a composite based on CoFe2O4 and BaTiO3 with piezoelectric and piezomagnetic properties is studied simultaneously.
Solutions to the problems of electroelasticity and magnetoelasticity are given in [9–11]. In [12], applied theories of vibrations of multilayer piezoelectric plates were developed considering the specifics of the distribution of electric potential over the structure thickness.
The problems on steady-state oscillations of an electro-magneto-elastic layer and a half-space under the action of harmonic loads are presented in [13][14]. The prestressing is taken into account, as well as various electrical and magnetic conditions at the boundaries. The effect of these factors on the dispersion properties is investigated. Earlier [15][16], an applied theory was developed that considers the inhomogeneous distribution of the electric potential in the longitudinal direction, and the quadratic dependence on thickness. In the same papers, the stress-strain and electrical state of a hinged and cantilevered bimorph is investigated. In both cases, the applied theory showed good convergence with the finite element modeling results. The authors also developed an applied theory of bimorph vibrations [17] consisting of an electroelastic and magnetoelastic layer. This approach is in good agreement with the finite element analysis results.
In this paper, the vibrations of the device are considered in the framework of a plane deformation. Based on the variational principle, an applied theory of bending vibrations of a two-layer piezoelectric bimorph is constructed. For steady-state vibrations, boundary conditions and a system of differential equations are obtained for four unknown functions (deflection, electric potential in the middle of the layer, magnetic potential in the middle of the layer and at the outer boundary), depending on the length of the bimorph. The influence of different percentage volume ratios of the bimorph composition on deflection, electric and magnetic potentials in certain positions, is investigated. The study results provide selecting the makeup of a composite piezomagnetoelectric material to achieve the most efficient operation of the device.
Materials and Methods. A plate consisting of two identical piezoelectric layers is considered. It performs steady-state transverse vibrations within a plane deformation. Each layer is a 2–2 connectivity composite consisting of alternating piezoelectric and piezomagnetic layers (Fig. 1).
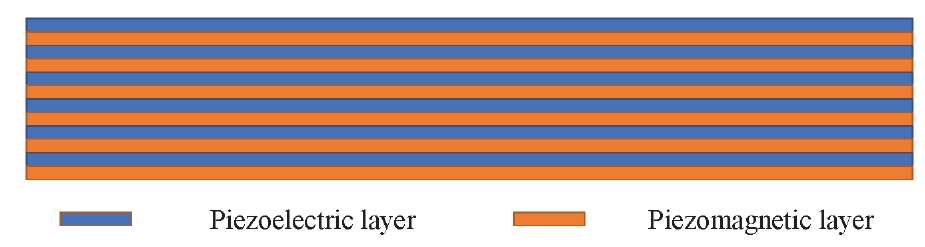
Fig. 1. 2-2 composite structure
Effective properties of such a composite were found in [8]. Large surfaces of the layers are electrodated, and the layers themselves are polarized in thickness. The bimorph is hinged at the edges, all surfaces are free from mechanical stresses. The upper and lower boundaries of the plate are affected by magnetic flux 0 B , while at the boundary between the layers, the magnetic potential is considered to be zero. The electrical potential is zero at all electrodes. The side surfaces are considered to be insulated from magnetic and electric fields.
The equations for describing the vibrations of a composite with effective properties, connectivity of mechanical, electric and magnetic fields, have the form [18]:
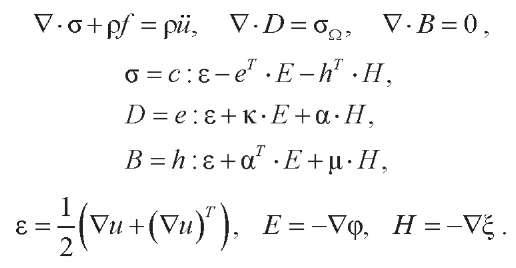 (1)
(1)
Here, σ and ε — mechanical stress and strain tensors, D and E — vectors of electric induction and electric field strength, B and H — vectors of magnetic induction and magnetic field strength, ρ — material density, c — elastic moduli tensor, e — piezoelectric moduli tensor, h — piezomagnetic moduli tensor, κ — dielectric permittivity tensor, α — magnetoelectric moduli tensor, μ — magnetic permeability tensor, f — mass force density vector, σΩ — electric charge volume density, u — displacement vector, φ and ξ — electrical and magnetic potentials.
The boundary conditions are determined for the mechanical, electric and magnetic fields, respectively.
For the first case, we note the absence of mechanical stresses at the bimorph boundary:
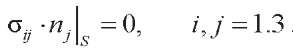
The biomorph is hinged at the ends (Fig. 2):
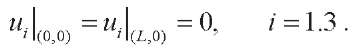
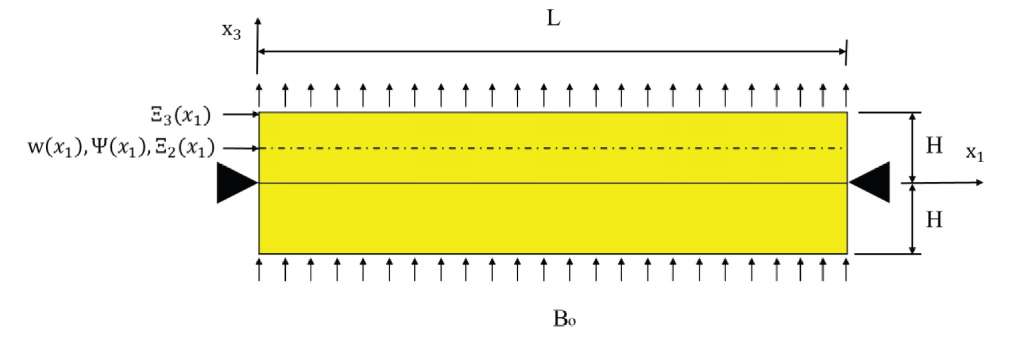
Fig. 2. Geometry and boundary conditions of bimorph
with composite piezomagnetoelectric layers
Next, we formulate the electrical boundary conditions. Electrical potential on the internal and external electrode, respectively:
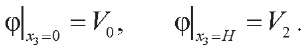
We indicate the magnetic boundary conditions. Magnetic potential at the inner boundary:
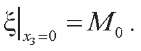
Magnetic flux B0 affects the upper and lower boundaries of the plate:
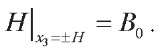
We use the variational equation for steady-state vibrations [10]. It generalizes Hamilton's principle in the electroelasticity theory taking into account magnetic components. For the case of plane deformation in the absence of surface loads and in the presence of magnetic flux:
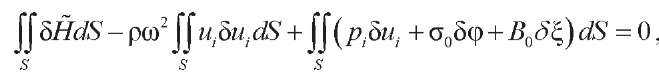 (2)
(2)
where δH̃ = σijδεij– DiδEi– BiδHi.
To construct an applied theory of vibrations, we will accept Kirchhoff's hypotheses. In accordance with them, the distribution of displacements along the thickness has the form:
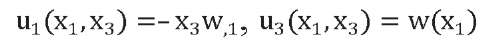 (3)
(3)
In particular, the single normal hypothesis is accepted for a mechanical field. Next, we consider a problem in which the value of the electric potential on the electrodes can be zero, so its distribution is not described by a linear function. Taking into account the possible inhomogeneity in the length of the element associated with the influence of boundary conditions at the ends of the bimorph, its thickness distribution is assumed to be quadratic:
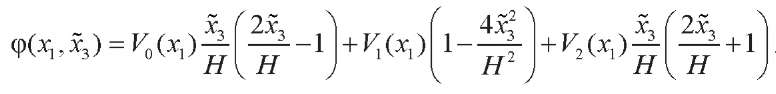 (4)
(4)
Here, x̃3 = x3– h/2. Functions V0, V1 and V2 are responsible for the value of the electric potential at the inner electrode, in the middle of the layer, and at the outer electrode, respectively. To satisfy the conditions of the problem, we take these functions in the following form (see Fig. 2):
Here, function Φ(x1) is unknown.
We represent a quadratic distribution of the magnetic potential over the thickness of each layer. The distribution along the length is heterogeneous, at the inner boundary of the layers, its value is assumed to be zero:
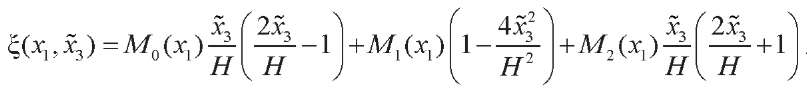 (5)
(5)
Here, x̃3 = x3– h/2. Functions M0, M1 and M2 are responsible for the value of the magnetic potential at the inner boundary, in the middle of the layer, and at the outer boundary, respectively, and are taken as follows (Fig. 2):
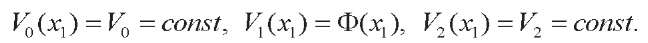
Here, functions 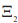 (x1) and
(x1) and 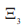 (x1) are unknown.
(x1) are unknown.
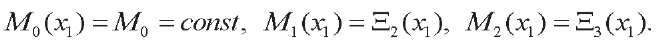
We substitute relations (3)–(5) into equation (2) and integrate it by the bimorph thickness, and then we equate the coefficients with independent variations δw, δΦ, δΞ2 and δΞ3 to zero. Thus, we obtain a system of four differential equations (6) from four unknown functions depending on х1 (then, we omit the subscript), and five boundary conditions (7).

Research Results. The results of the bimorph calculation according to the proposed theory are compared to the finite element calculation in the low-frequency region for the volume ratio of the piezoelectric and piezomagnetic components 80 % BaTiO3 and 20 % CoFe2O4. The comparison has shown that the error in finding the characteristics of the mechanical and magnetic fields is less than 1%. When determining the electric field in the middle part of the plate, the difference was about 5%. Describing the situation in the vicinity of the support points, it should be noted that the size of the neighborhood along the longitudinal coordinate is approximately equal to the bimorph thickness. Here, when determining the electric field, a difference of 20% is recorded.
The first step in studying the vibrations of a two-layer piezomagnetoelectric bimorph with a change in the volume ratio of BaTiO3 and CoFe2O4 in the composite is to determine its effective properties. Tables 1 and 2 present these properties found from the results of study [8].
Table 1
Material constants (elastic modules, dielectric and magnetic permittivity)
for different BaTiO3 volume fraction
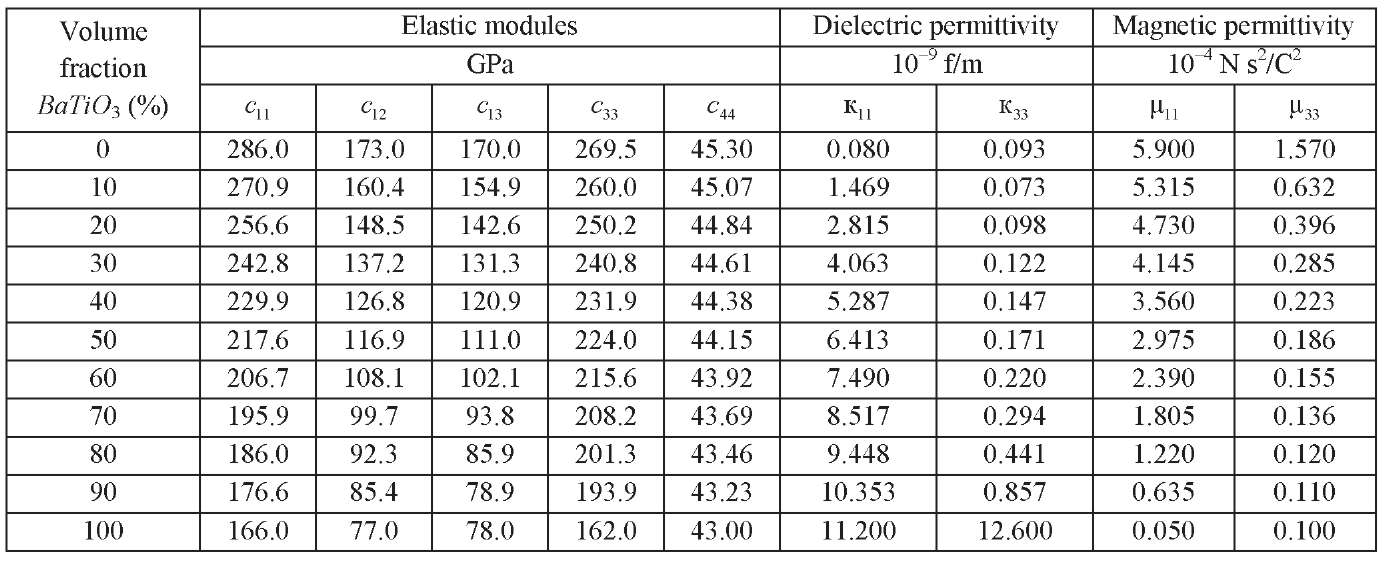
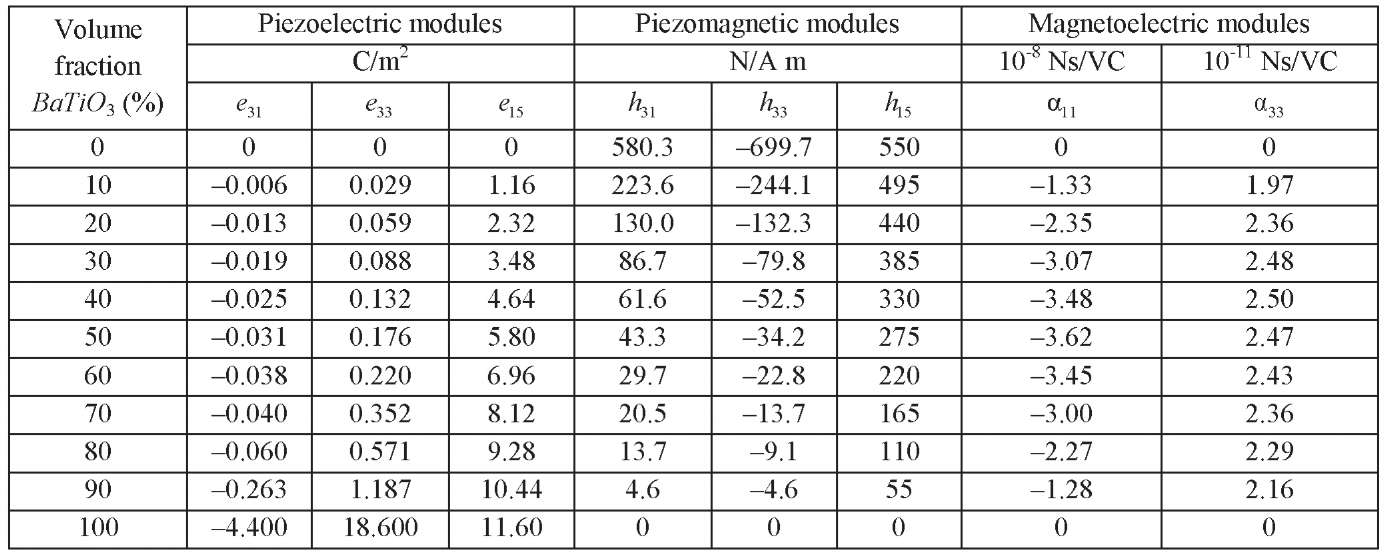
Table 2
Material constants (piezoelectric, piezomagnetic and magnetoelectric modules)
for different BaTiO3 volume fraction
The bimorph vibrations were excited by a magnetic flux applied to the upper and lower faces (Fig. 2), which varied according to the harmonic law with an amplitude of B0=5 ×10-5 Wb and a frequency of 10 kHz.
Figure 3 shows the deflection in the middle of the layer depending on volume fraction of BaTiO3. It can be seen from the graph that the deflection in the position having coordinates x1 = L / 2, x3 = H / 2, is zero if the bimorph consists only of a piezoelectric BaTiO3. The deflection of the bimorph reaches the greatest value if it contains only piezoelectric magnet CoFe2O4. The deflection almost linearly depends on the volume ratio of the components of piezoactive materials.
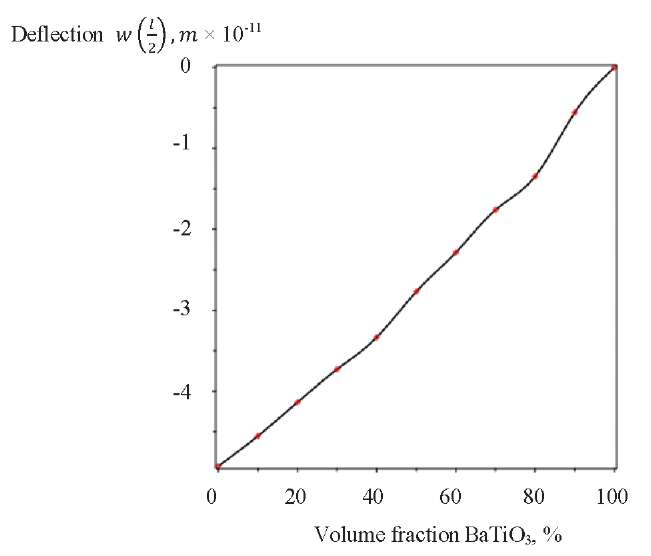
Fig. 3. Deflection w(x1) in the middle of the layer for different BaTiO3 volume fraction
Based on the data in Figure 4, it can be concluded that the electric potential in the middle of the layer varies nonlinearly with a change in the volume ratio of the composition of bimorph piezoactive materials. If the bimorph consists only of BaTiO3 or CoFe2O4, then the electric potential at the point (L / 2, Н / 2) is zero and reaches the highest value at 35 % BaTiO3 in the bimorph.
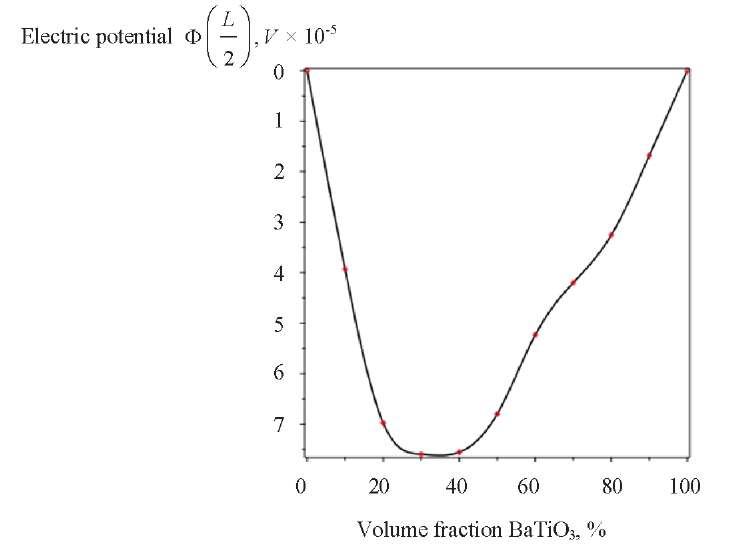
Fig. 4. Electric potential 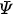 (x1 ) for different BaTiO3 volume fraction
(x1 ) for different BaTiO3 volume fraction
The analysis of Figures 5 and 6 allows us to conclude that the magnetic potential in the middle of the layer 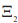 (L / 2) and at the outer boundary
(L / 2) and at the outer boundary 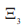 (L / 2) increases almost linearly with an increase in the volume of BaTiO3 in the bimorph.
(L / 2) increases almost linearly with an increase in the volume of BaTiO3 in the bimorph.
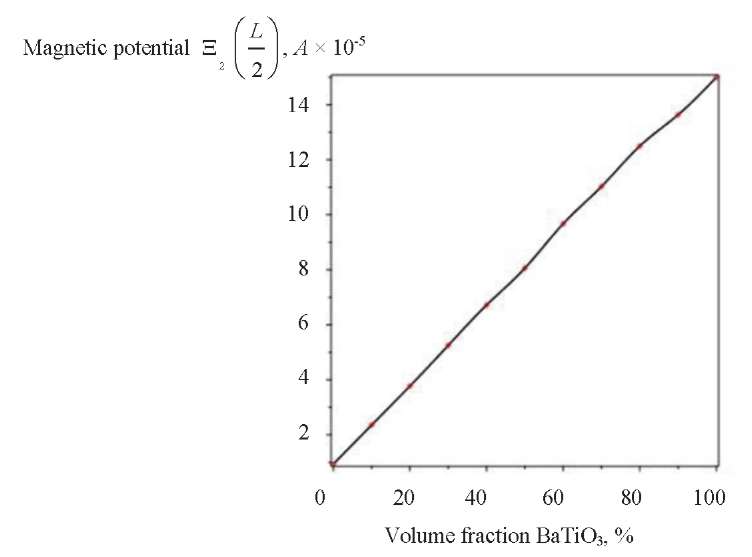
Fig. 5. Magnetic potential 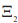 (L / 2) for different BaTiO3 volume fraction
(L / 2) for different BaTiO3 volume fraction
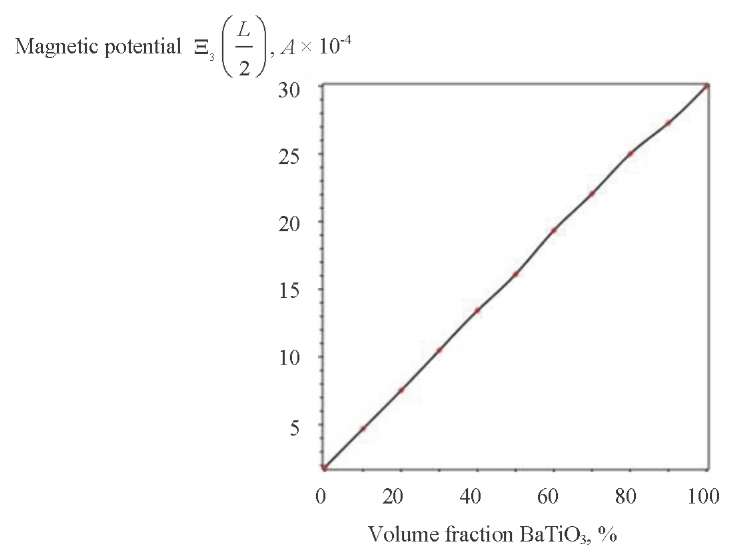
Fig. 6. Magnetic potential 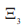 (L / 2) for different BaTiO3 volume fraction
(L / 2) for different BaTiO3 volume fraction
Discussion and Conclusions. An applied theory is proposed for calculating transverse vibrations of a bimorph made of two layers of a composite based on CoFe2O4 and BaTiO3 with both piezoelectric and piezomagnetic properties, in an alternating magnetic field. Such a design can serve as a model of a piezoelectric generator of a device for collecting and storing energy under the action of an external magnetic field. In the low-frequency region (below the natural frequency of the first bending mode), calculations of the stress-strain state of the bimorph, the distribution of electric and magnetic fields, are carried out. The dependence of the deflection, electric and magnetic potentials on the volume ratio of the bimorph composition is investigated. In further work, it is assumed to determine the output potential and power of an electric current excited by an alternating magnetic field. The purpose of these surveys will be to collect electrical energy.
References
1. Gaudenzi, P. Smart structures: physical behavior, mathematical modeling and applications / Paolo Gaudenzi. — New York : John Wiley & Sons, 2009. — 194 p. https://doi.org/10.1002/9780470682401
2. A review of smart materials: Researches and applications / I. N. Qader, M. Kok, F. Dagdelen, Y. Aydogdu // El-Cezeri Journal of Science and Engineering. — 2019. — Vol. 6. — P. 755–788. https://doi.org/10.31202/ecjse.562177
3. Crafting the multiferroic BiFeO3 -CoFe2O4 nanocomposite for next-generation devices: A review / T. Amrillah, A. Hermawan, C. P. Wulandari [et al.] // Materials and Manufacturing Processes. — 2021. — Vol. 36. — P. 1579–1596. https://doi.org/10.1080/10426914.2021.1945096
4. Tunable maximum energy product in CoFe2O4 nanopowder for permanent magnet application / B. Abraime, A. Mahmoud, F. Boschini [et al.] // Journal of Magnetism and Magnetic Materials. — 2018. — Vol. 467. — P. 129–134. https://doi.org/10.1016/j.jmmm.2018.07.063
5. Size effect on the magnetic properties of CoFe2O4 nanoparticles: a Monte Carlo study / R. Lamouri, O. Mounkachi, E. Salmani [et al.] // Ceramics International. — 2020. — Vol. 46. — P. 8092–8096. https://doi.org/10.1016/j.ceramint.2019.12.035
6. Kim, J.-Y. Micromechanical analysis of effective properties of magneto-electro-thermo-elastic multilayer composites / Jin-Yeon Kim // International Journal of Engineering Science. — 2011. — Vol. 49. — P. 1001–1018. https://doi.org/10.1016/j.ijengsci.2011.05.012
7. Siva, K. V. Improved room temperature magnetoelectric response in CoFe2O4-BaTiO3 core shell and bipolar magnetostrictive properties in CoFe2O4 / K. V. Siva, P. Kaviraj, A. Arockiarajan // Materials Letters. — 2020. Vol. 268. — Art. 127623. https://doi.org/10.1016/j.matlet.2020.127623
8. Challagulla, K. S. Micromechanical analysis of magneto-electro-thermo-elastic composite materials with applications to multilayered structures / K. S. Challagulla, A. V. Georgiades // International Journal of Engineering Science. — 2011. — Vol. 49. — P. 85–104. https://doi.org/10.1016/j.ijengsci.2010.06.025
9. Новацкий, В. Электромагнитные эффекты в твердых телах / В. Новацкий, В. А. Шачнев. — Москва : Мир, 1986. — 160 с.
10. Партон, В. З. Электромагнитоупругость пьезоэлектрических и электропроводных тел / В. З. Партон, Б. А. Кудрявцев // Москва : Наука, 1988. — 472 с.
11. Багдасaрян, Г. Е. Электромагнитоупругие волны / Г. Е. Багдасaрян, З. Н. Даноян. — Ереван : Изд-во Ереванского государственного университета, 2006. — 492 с.
12. Vatul'yan, A. O. Flexural vibrations of a piezoelectric bimorph with a cut internal electrode / A. O. Vatul'yan, A. A. Rynkova // Journal of Applied Mechanics and Technical Physics. — 2001. — Vol. 42. — P. 164–168. https://doi.org/10.1023/A:1018837401827
13. Levi, M. O. Some features of the dynamics of electro-magneto-elastic half-space with initial deformations / M. O. Levi, V. V. Kalinchuk // In: Proc. 2017 Dynamics of Systems, Mechanisms and Machines (Dynamics), IEEE. 2017. — P. 262–266. https://ieeexplore.ieee.org/document/8239478
14. Влияние граничных условий на динамику электромагнитоупругой полуограниченной среды / М. О. Леви, И. Е. Анджикович, Е. И. Ворович, И. Б. Михайлова // Вестник Южного научного центра РАН. 2012. — T. 8, № 4. — C. 14–19.
15. Applied theory of bending vibrations of a piezoelectric bimorph with a quadratic electric potential distribution / A. N. Soloviev, V. A. Chebanenko, I. A. Parinov, P. A. Oganesyan // Materials Physics and Mechanics. 2019. — Vol. 42. — P. 65–73. https://doi.org/10.18720/MPM.4212019_7
16. Исследование колебаний биморфной пластины с учетом нелинейности электрического потенциала / А. Н. Соловьев, В. А. Чебаненко, И. А. Паринов, П. А. Оганесян // Наука Юга России. — 2019. — Т. 15, № 3. С. 3–11. https://doi.org/10.7868/S25000640190301
17. Applied theory of bending vibration of the piezoelectric and piezomagnetic bimorph / Do Thanh Binh, V. A. Chebanenko, Le Van Duong [et al.] // Journal of Advanced Dielectrics. — 2020. — Vol. 10. — Art. 2050007. https://doi.org/10.1142/S2010135X20500071
18. Finite element approach for composite magneto-piezoelectric materials modeling in ACELAN-COMPOS package / N. V. Kurbatova, D. K. Nadolin, A. V. Nasedkin [et al.] // In book: Analysis and Modelling of Advanced Structures and Smart Systems. — 2018. — Vol. 81. — P. 69–88. https://doi.org/10.1007/978-981-10-6895-9_5
About the Authors
A. N. SolovievRussian Federation
Arkadiy N. Soloviev
Rostov-on-Don
Thanh Binh Do
Russian Federation
Rostov-on-Don
V. A. Chebanenko
Russian Federation
Valerii A. Chebanenko
Rostov-on-Don
O. N. Lesnyak
Russian Federation
Olga N. Lesnyak
Rostov-on-Don
E. V. Kirillova
Germany
Evgeniya V. Kirillova
Wiesbaden
Review
For citations:
Soloviev A.N., Do T., Chebanenko V.A., Lesnyak O.N., Kirillova E.V. Vibration analysis of a composite magnetoelectroelastic bimorph depending on the volume fractions of its components based on applied theory. Advanced Engineering Research (Rostov-on-Don). 2022;22(1):4-13. https://doi.org/10.23947/2687-1653-2022-22-1-4-13




































